In questo esercizio ci proponiamo di dare la risoluzione di una travatura reticolare isostatica, discutendo staticamente e cineticamente, determinando gli sforzi normali nelle aste e calcolandone lo spostamento del nodo G. Le singole barre orizzontali e verticali sono di lunghezza generica l, mentre le aste AC, CE e EG sono soggette ad un carico distribuito di valore fittizio q.
La struttura reticolare è composta da 5 aste e 6 nodi. I vincoli esterni sono due cerniere. Pertanto possiamo scrivere:
Vc = QL/2

NODO F
↑ - N6 ∙ √2/2 - QL - QL/√2 ∙ 1/√2= 0
↑ N10∙ 5√2/2 - 1 = 0
N10 = √2
↑ N8 = 0

NODO C
↑ N2∙ √2/2 - √2∙ √2/2= 0
N2 = √2
SPOSTAMENTO
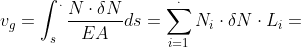
&space;QL&space;+&space;(2&space;\cdot&space;2&space;)&space;QL&space;+&space;0&space;+&space;\left&space;(&space;-\frac{1}{2}&space;\cdot&space;-1&space;\right&space;)&space;QL&space;+&space;4&space;\left&space;(&space;0&space;+&space;\frac{1}{2}&space;QL&space;\right&space;)+)
\right&space;)&space;\cdot&space;\frac{1}{EA}&space;=)
+&space;\sqrt{2}QL^2&space;\cdot&space;(5+3+1))&space;\right&space;)\frac{1}{EA}&space;=)
\frac{QL^2}{EA}=)
&space;\frac{QL^2}{EA})
Strutture
Sistema principale
na = 10
nn = 7
ne= nA+nB = 2 + 2 = 4
na + ne = 14
nn = 7x2 = 14
Visto che il risultato (14-14=0) è nullo, la struttura reticolare risulta essere isostatica.
Passare da carico distribuito a carico concentrato
Le aste AC, CE e EG, sono soggette ad un carico distribuito, sia da un punto di vista teorico che pratico, non si può procedere alla risoluzione della nostra trave usando questo tipo di carico. Si deve trovare un carico concentrato che agisce sui nodi. Ci è permesso in questo caso, di trascurare le forze di taglio e momento che agiscono sulle tre aste, perché comunque questo non viene trasmesso.
SISTEMA REALE
NODO G

NODO F
↑ - N6 ∙ √2/2 - QL - QL/√2 ∙ 1/√2= 0
→ -N7 + QL/√2 ∙ √2/2 - N6 ∙ √2/2 = 0
N7 = 2QL
NODO D
↑ N4 = 0
N7 = 2QL
NODO D
↑ N4 = 0
SISTEMA VIRTUALE
Procediamo alla risoluzione della travatura reticolare del sistema virtuale, dove è stato inserito il carico virtuale 1, che determinerà i risultati.
N10 = √2
→ - N9 - √2 ∙√2/2 = 0
N9 = -1
N9 = -1

NODO C
↑ N2∙ √2/2 - √2∙ √2/2= 0
N2 = √2
→ -N1 - 1 - 1 - 1 = 0
N1 = -3
N1 = -3
Asta
|
L
|
N
|
δN
|
1
|
L
|
-9/2 QL
|
-3
|
2
|
√2L
|
5√2/2 QL
|
√2
|
3
|
L
|
2QL
|
2
|
4
|
L
|
0
|
0
|
5
|
L
|
-QL/2
|
-1
|
6
|
√2L
|
-3√2/2 QL
|
-√2
|
7
|
L
|
2QL
|
-2
|
8
|
L
|
QL
|
0
|
9
|
L
|
-QL/2
|
-1
|
10
|
√2l
|
√2QL/2
|
√2
|
SPOSTAMENTO












