La struttura reticolare presa in considerazione è una trave composta da 21 nodi e 39
aste indispensabili quindi la struttura risulta indeformabile. Per risolvere la struttura
vengono fatte delle ipotesi semplificative:
– Le aste, i vincoli e i carichi gravanti sulla struttura sono tutti complanari; – I carichi esterni sono applicati unicamente ai nodi;
– I nodi che collegano le aste sono cerniere;
La struttura è simmetrica quindi l'analisi delle reazioni viene fatta solo su metà di essa. Le aste sono soggette a sollecitazioni di tipo assiale, che causeranno trazione (tiranti) o compressione (puntoni) dipendente dal verso della sollecitazione.
Analisi dei carichi agenti sui nodi
I carichi agenti sui nodi sono le reazioni vincolari trasmesse loro dalla trave secondaria, sommato al peso del corrimano che viene ancorato nei punti dei nodi. Il peso del corrimano viene considerato fittizio di 0,5 kN.
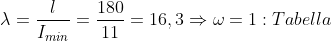
– Le aste, i vincoli e i carichi gravanti sulla struttura sono tutti complanari; – I carichi esterni sono applicati unicamente ai nodi;
– I nodi che collegano le aste sono cerniere;
La struttura è simmetrica quindi l'analisi delle reazioni viene fatta solo su metà di essa. Le aste sono soggette a sollecitazioni di tipo assiale, che causeranno trazione (tiranti) o compressione (puntoni) dipendente dal verso della sollecitazione.
Analisi dei carichi agenti sui nodi
I carichi agenti sui nodi sono le reazioni vincolari trasmesse loro dalla trave secondaria, sommato al peso del corrimano che viene ancorato nei punti dei nodi. Il peso del corrimano viene considerato fittizio di 0,5 kN.
Quindi avremo:
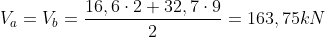
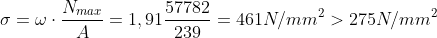
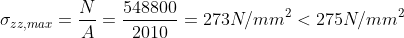
Risulta verificata
Per la simmetria avremo da risolvere i seguenti 11 nodi:
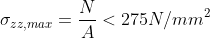
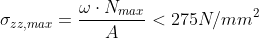
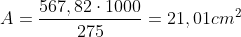
Dimensionamento delle aste della trave
Le aste risultano sollecitate esclusivamente a sforzo normale, essendo trascurabile il momento flettente dovuto al peso proprio.Per i tiranti la verifica di resistenza è soddisfatta dalla seguente equazione:
Le aste risultano sollecitate esclusivamente a sforzo normale, essendo trascurabile il momento flettente dovuto al peso proprio.Per i tiranti la verifica di resistenza è soddisfatta dalla seguente equazione:
Per i puntoni la verifica viene effettuata secondo il metodo “ω”. In questo caso la formula
precedente diviene:
Dove “ω” è un coefficiente maggiore dell’unità, che tende al valore di 1 per strutture poco snelle
(tozze) mentre per snellezze elevate dipende dalle caratteristiche del materiale impiegato, dalla
snellezza dell’elemento considerato, e quindi dalla geometria della sezione trasversale, dalla
lunghezza della trave e dai vincoli di estremità.
Asta orizzontale maggiormente soggetta a compressione:
Puntone 10 – 12 => 567,82 kN
Asta orizzontale maggiormente soggetta a compressione:
Puntone 10 – 12 => 567,82 kN
Risulta verificata
Verifica di stabilità a carico di punta





