CONTROVENTATURE
ANALISI DEI CARICHI
Calcolo della superficie sottoposta ad azione orizzontale:
Calcolo della superficie sottoposta ad azione orizzontale:
Aste orizzonatli
|
18 x 1840 + 18 x 1640 = 62'640
|
Aste diagonali
|
5 x 113 x 20 = 45'200
|
Piatti
|
40 x 20 x 20 = 16'000
|
Parapetto, considerato pieno
|
1840 x 120 = 220'800
|
Totale
|
344'640 cm2 = 34,464 m2 |
Avendo già identificato l'azione del vento p: p=356 N/m = 0,356 kN/m
In totale si ha:
Quindi, inserendo i controventi tra ogni trave secondaria si riesce a calcolare il carico
concentrato rispetto all'area di influenza.
w = 1,226 x 1,8 = 2,21 kN
we = 1,226 x 0,9 = 1,111 kN V = 6,1 kN
Il carico è aggravato dal coefficiente dovuto al sovraccarico principale.
V = 6,1 x 1,5 = 9,15 kN
Si procede con il metodo di calcolo basato sull'equilibrio dei nodi, usando la procedura di calcolo del poligono di equilibrio. Considerando che l'asta compressa si instabilizzi e che quindi non assorba più lo sforzo normale.
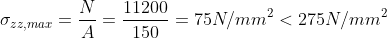
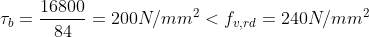
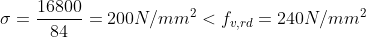
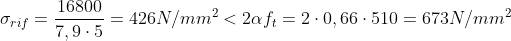
w = 1,226 x 1,8 = 2,21 kN
we = 1,226 x 0,9 = 1,111 kN V = 6,1 kN
Il carico è aggravato dal coefficiente dovuto al sovraccarico principale.
V = 6,1 x 1,5 = 9,15 kN
Si procede con il metodo di calcolo basato sull'equilibrio dei nodi, usando la procedura di calcolo del poligono di equilibrio. Considerando che l'asta compressa si instabilizzi e che quindi non assorba più lo sforzo normale.
La distribuzione dei carichi, tenendo conto della simmetria della struttura sarà quindi.
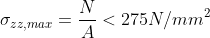
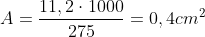
Dimensionamento delle aste della trave
Le aste risultano sollecitate esclusivamente a sforzo normale, essendo trascurabile il momento flettente dovuto al peso proprio. Per i tiranti la verifica di resistenza è soddisfatta dalla seguente equazione:
Le aste risultano sollecitate esclusivamente a sforzo normale, essendo trascurabile il momento flettente dovuto al peso proprio. Per i tiranti la verifica di resistenza è soddisfatta dalla seguente equazione:
Asta diagonale maggiormente soggetta a trazione:
Tirante 2 - 3 => 11,2 kN
Profilo appropriato: Piatto 30 x 5
Verifica a resistenza
Area= 1,50 cm2
L= 415 cm
L= 415 cm
Verifica a resistenza
COLLEGAMENTO
Si considera l'asta maggiormente tesa per dimensionare il giunto.
Consideriamo un bullone M12-Cl 8.8
S 2-3 = 11,2 x 1,5 = 16,8 kN
Verifica bullone
Si considera l'asta maggiormente tesa per dimensionare il giunto.
Consideriamo un bullone M12-Cl 8.8
S 2-3 = 11,2 x 1,5 = 16,8 kN
Verifica bullone
Verifica piastra
Per tesare le diagonali si adotterà un tenditore con un carico di rottura pari a 18 kN.
La verifica a rifollamento va fatta in corrispondenza del tenditore essendo il diametro
A 150 della vite delle ganasce inferiore a quello del bullone; nel nostro caso avremo:
Le verifiche sono soddisfatte. Si adotterà la stessa sezione per tutte le diagonali.
COLLEGAMENTI
Trave principale – Trave secondaria
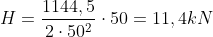
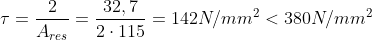
Verifica delle squadrette
}=12,7&space;N/mm^2)
&space;+&space;7&space;\cdot&space;\frac{14^3}{12}&space;\right&space;)&space;\right&space;)/90}=100&space;N/mm^2)
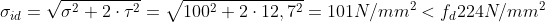
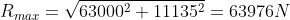
Strutture
Bulloni MT14-CL 8.8
Ra = Rb = 32,7 kN
V = 32,7 kN
M1 = 32,7 x 35 = 1144,5 kNmm
Che danno luogo nei bulloni alle seguenti forze:
V= 32,7 / 2 = 16,35 kN
Ra = Rb = 32,7 kN
V = 32,7 kN
M1 = 32,7 x 35 = 1144,5 kNmm
Che danno luogo nei bulloni alle seguenti forze:
V= 32,7 / 2 = 16,35 kN
Verifica delle squadrette
STUDIO STATICO DELLA STRUTTURA RETICOLARE
La struttura reticolare presa in considerazione è una trave composta da 21 nodi e 39
aste indispensabili quindi la struttura risulta indeformabile. Per risolvere la struttura
vengono fatte delle ipotesi semplificative:
– Le aste, i vincoli e i carichi gravanti sulla struttura sono tutti complanari; – I carichi esterni sono applicati unicamente ai nodi;
– I nodi che collegano le aste sono cerniere;
La struttura è simmetrica quindi l'analisi delle reazioni viene fatta solo su metà di essa. Le aste sono soggette a sollecitazioni di tipo assiale, che causeranno trazione (tiranti) o compressione (puntoni) dipendente dal verso della sollecitazione.
Analisi dei carichi agenti sui nodi
I carichi agenti sui nodi sono le reazioni vincolari trasmesse loro dalla trave secondaria, sommato al peso del corrimano che viene ancorato nei punti dei nodi. Il peso del corrimano viene considerato fittizio di 0,5 kN.
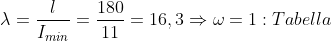
– Le aste, i vincoli e i carichi gravanti sulla struttura sono tutti complanari; – I carichi esterni sono applicati unicamente ai nodi;
– I nodi che collegano le aste sono cerniere;
La struttura è simmetrica quindi l'analisi delle reazioni viene fatta solo su metà di essa. Le aste sono soggette a sollecitazioni di tipo assiale, che causeranno trazione (tiranti) o compressione (puntoni) dipendente dal verso della sollecitazione.
Analisi dei carichi agenti sui nodi
I carichi agenti sui nodi sono le reazioni vincolari trasmesse loro dalla trave secondaria, sommato al peso del corrimano che viene ancorato nei punti dei nodi. Il peso del corrimano viene considerato fittizio di 0,5 kN.
Quindi avremo:
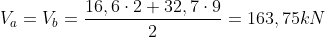
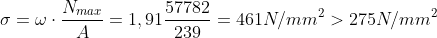
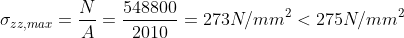
Risulta verificata
Per la simmetria avremo da risolvere i seguenti 11 nodi:
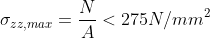
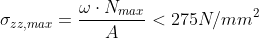
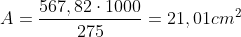
Dimensionamento delle aste della trave
Le aste risultano sollecitate esclusivamente a sforzo normale, essendo trascurabile il momento flettente dovuto al peso proprio.Per i tiranti la verifica di resistenza è soddisfatta dalla seguente equazione:
Le aste risultano sollecitate esclusivamente a sforzo normale, essendo trascurabile il momento flettente dovuto al peso proprio.Per i tiranti la verifica di resistenza è soddisfatta dalla seguente equazione:
Per i puntoni la verifica viene effettuata secondo il metodo “ω”. In questo caso la formula
precedente diviene:
Dove “ω” è un coefficiente maggiore dell’unità, che tende al valore di 1 per strutture poco snelle
(tozze) mentre per snellezze elevate dipende dalle caratteristiche del materiale impiegato, dalla
snellezza dell’elemento considerato, e quindi dalla geometria della sezione trasversale, dalla
lunghezza della trave e dai vincoli di estremità.
Asta orizzontale maggiormente soggetta a compressione:
Puntone 10 – 12 => 567,82 kN
Asta orizzontale maggiormente soggetta a compressione:
Puntone 10 – 12 => 567,82 kN
Risulta verificata
Verifica di stabilità a carico di punta
Iscriviti a:
Commenti (Atom)
Questo lavoro è il risultato finale di un laboratorio del corso di Tecnica delle costruzioni dell'Università di Genova. Ho preferito condividerlo che lasciarlo morire nel computer.















